Faktor / komponens pontszámok kiszámításának módszerei
Megjegyzéssorozat után úgy döntöttem, hogy végül választ adok (a megjegyzések és egyebek alapján). Komponens pontszámok kiszámításáról szól PCA-ban és faktor-pontszámokról a faktoranalízisben.
A faktor / komponens pontszámokat a $ \ bf \ hat {F} = XB $ adja meg, ahol $ \ bf X $ az elemzett változók ( központosítva , ha a PCA / faktor elemzés kovarián alapult, vagy z-standardizált , ha összefüggéseken alapult). $ \ bf B $ a faktor / komponens pontszám koefficiens (vagy súly) mátrix . Hogyan becsülhetők meg ezek a súlyok?
Jelölés
$ \ bf R $ - pxp változó (elem) összefüggések vagy kovarianciák mátrixa, attól függően, hogy melyik tényező volt / A PCA elemzésre került.
$ \ bf P $ - pxm faktor / komponens betöltések mátrixa. Ezek lehetnek az extrakció utáni terhelések (gyakran $ \ bf A $ jelöléssel is), ekkor a látensek ortogonálisak vagy gyakorlatilag ilyenek, vagy rotáció utáni terhelések, ortogonálisak vagy ferdeek. Ha az elforgatás ferde, akkor minta betöltésnek kell lennie.
$ \ bf C $ - mxm korrelációk mátrixa a tényezők / alkatrészek között (a terhelések) ferde forgatásuk után. Ha nem végeztek el ortogonális elforgatást, akkor ez az azonosság mátrix.
$ \ bf \ hat R $ - pxp a reprodukált korrelációk csökkentett mátrixa / kovariancia, $ \ bf = PCP '$ ($ \ bf = PP' $ az ortogonális megoldásokhoz), átlóján kommunalitásokat tartalmaz.
$ \ bf U_2 $ - pxp az egyediségek átlós mátrixa (egyediség + közösségiség = $ \ bf R $ átlós eleme). Itt a "2" -t használom indexként felső index ($ \ bf U ^ 2 $) helyett az olvashatóság érdekében a képletekben.
$ \ bf R ^ * $ - pxp a reprodukált összefüggések / kovariancia teljes mátrixa, $ \ bf = \ hat R + U_2 $.
$ \ bf M ^ + $ - valamilyen mátrix álverse $ \ bf M $; ha $ \ bf M $ teljes rangú, $ \ bf M ^ + = (M'M) ^ {- 1} M '$.
$ \ bf M ^ {power} $ - bizonyos négyzet alakú szimmetrikus mátrixok esetében $ \ bf M $, $ emelés $ power $ -ra azt jelenti, hogy a $ \ bf HKH '= M $ összeadódik, a sajátértékeket a hatványra emeli és vissza komponálja : $ \ bf M ^ {power} = HK ^ {power} H '$.
Durva módszer a tényező / komponens pontszámának kiszámításához
Ez a népszerű / hagyományos megközelítés, amelyet néha Cattell-nek is hívnak , egyszerűen ugyanazon tényező által betöltött elemek átlagolása (vagy összegzése). Matematikailag a $ \ bf B = P $ súlyok beállítását jelenti a $ \ bf \ hat {F} = XB $ pontszámok kiszámításakor. A megközelítésnek három fő változata van: 1) Használja a terheléseket úgy, ahogy vannak; 2) Dichotomizálja őket (1 = betöltve, 0 = nincs betöltve); 3) Használja a terheléseket úgy, ahogy vannak, de nulla terhelés kisebb, mint valamilyen küszöbérték.
Ezzel a megközelítéssel gyakran, ha az elemek ugyanazon a skálaegységen vannak, a $ \ bf X $ értékeket csak nyersen használják; bár a faktoring logikájának megsértése érdekében jobb lenne használni a $ \ bf X $ értéket, mivel belépett a faktoringba - standardizált (= korrelációk elemzése) vagy központosított (= kovariancia elemzés).
A fő hátrány a durva módszerrel számolási tényező / komponens pontszámok véleményem szerint az, hogy nem veszi figyelembe a betöltött elemek közötti összefüggéseket. Ha egy tényezővel terhelt elemek szorosan korrelálnak, és az egyiket erősebben töltik be, mint a másikat, ez utóbbi ésszerűen fiatalabb duplikátumnak tekinthető, és súlya csökkenthető. Finomított módszerek csinálják, de a durva módszer nem.
A durva pontszámokat természetesen könnyű kiszámítani, mert nincs szükség mátrix inverzióra. A durva módszer előnye (megmagyarázva, hogy a számítógépek rendelkezésre állása ellenére miért használják még mindig széles körben), hogy mintánként stabilabb pontszámokat ad, ha a mintavétel nem ideális (reprezentativitás és méret szempontjából), vagy elemzés nem volt megfelelő. Egy cikket idézve: "Az összesített pontszám módszer akkor lehet a legkívánatosabb, ha az eredeti adatok összegyűjtésére használt skálák teszteletlenek és feltáró jellegűek, a megbízhatóság vagy az érvényesség bizonyítéka alig vagy egyáltalán nincs". Emellett nem szükséges megérteni a "faktort" szükségszerűen egyváltozós látens esszenciának, mivel a faktoranalízis modell megköveteli ( lásd, lásd). Például elképzelhet egy faktort jelenségek gyűjteményeként - akkor az elemértékek összegzése ésszerű.
Finomított módszerek a tényező / komponens pontszámok kiszámítására
Ezek a módszerek faktorelemző csomagok teszik. Különböző módszerekkel becsülik a $ \ bf B $ értéket. Míg a $ \ bf A $ vagy $ \ bf P $ betöltések a lineáris kombinációk együtthatói a változók tényezők / összetevők szerinti előrejelzéséhez, addig a $ \ bf B $ azok a tényezők, amelyek kiszámítják a tényezők / komponensek pontszámát a változókból.
A $ \ bf B $ segítségével kiszámított pontszámok skálázódnak: szórásaik egyenlőek vagy közel 1-vel vannak (standardizáltak vagy közel standardizáltak) - nem a valódi tényező-eltérések (amelyek megegyeznek a négyzet alakú szerkezeti terhelések összegével, lásd a 3. lábjegyzetet itt). Tehát, ha a tényező pontszámokat a valódi tényező varianciájával kell ellátni, szorozza meg a pontszámokat (standardizálva őket 1. szórásra) a variancia négyzetgyökével.
Megtarthatja a $ \ bf B $ értéket az elvégzett elemzésből, hogy kiszámíthassa a $ \ bf X $ új megfigyeléseinek pontszámait. A $ \ bf B $ felhasználható a kérdőív skáláját alkotó elemek súlyozására is, ha a skálát faktoranalízis alapján fejlesztik ki vagy validálják. A $ \ bf B $ (négyzet) együtthatói úgy értelmezhetők, mint az elemek hozzájárulása a tényezőkhöz. Az együtthatók úgy standardizálhatók, mint a regressziós együttható szabványosítása $ \ beta = b \ frac {\ sigma_ {item}} {\ sigma_ {factor}} $ (ahol $ \ sigma_ {factor} = 1 $), hogy összehasonlítsák a különböző elemek hozzájárulásait eltérések.
Lásd egy példát, amely a PCA-ban és az FA-ban végzett számításokat mutatja be, beleértve a pontszámok kiszámítását a pontszám-együttható mátrixból.
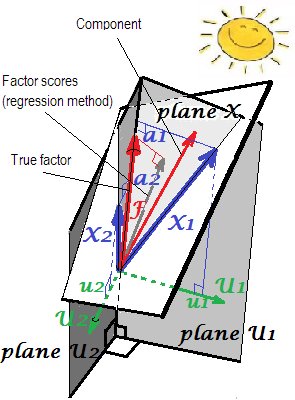
A terhelések geometriai magyarázata A $ a $ (merőleges koordinátaként) és a pontszám együtthatók $ b $ s (ferde koordináták) a PCA beállításaiban az első két képen itt láthatók.
Most a finomított módszerek.
A módszerek
$ \ bf B $ kiszámítása PCA-ban
Ha az alkatrészterheléseket kivonják, de nem forgatják, akkor $ \ bf B = AL ^ {- 1} $, ahol $ \ bf L $ az átlós mátrix, amely m sajátértékekből áll; ez a képlet annyit jelent, hogy egyszerűen elosztjuk a $ \ bf A $ minden oszlopát a megfelelő sajátértékkel - az összetevő varianciájával.
Ekvivalens módon $ \ bf B = (P ^ +) '$. Ez a képlet az ortogonálisan (például a varimax) vagy ferdén elforgatott alkatrészekre (terhelésekre) is vonatkozik.
A faktoranalízis során alkalmazott néhány módszer (lásd alább), ha a PCA-ban alkalmazzák, ugyanazt az eredményt adja vissza. / p>
A kiszámított összetevői pontszámok szórása 1 és az összetevők valódi standardizált értéke .
A statisztikai adatok elemzésében a $ \ bf B $ főkomponens-együttható mátrixot nevezzük, és ha a teljes pxp és nem is forgatott betöltési mátrixból számoljuk, akkor a gépi tanulásban az irodalmat gyakran felcímkézzük. a (PCA-alapú) fehérítő mátrixot és a szabványosított fő összetevőket "fehérített" adatokként ismerik fel.
$ \ bf B $ kiszámítása gyakori faktorelemzés
A komponens pontszámokkal ellentétben a faktor pontszámok soha nem pontosak ; csak a tényezők $ \ bf F $ ismeretlen valódi értékeihez közelítenek. Ez azért van, mert nem ismerjük a kommunalitások értékeit vagy az egyediséget esetszinten, - mivel a tényezők az összetevőktől eltérően külső változók, amelyek elkülönülnek a nyilvánvalóaktól, és rendelkeznek saját, számunkra ismeretlen eloszlással. Ez az oka annak, hogy a faktor határozatlanságot eredményezi. Ne feledje, hogy a határozatlansági probléma logikailag független a faktor megoldás minőségétől: az, hogy egy tényező mennyi igaz (megfelel annak a látensnek, amely generálja az adatokat a populációban), az más kérdés, mint az, hogy a válaszadók egy tényező pontszáma mennyire igaz (pontos becslések)
Mivel a faktor pontszámok közelítések, alternatív módszerek léteznek azok kiszámítására és versenyeznek.
Regresszió vagy Thurstone vagy Thompson módszere a becsléshez A faktor pontszámokat $ \ bf B = R ^ {- 1} PC = R ^ {- 1} S $ adja meg, ahol $ \ bf S = PC $ a struktúraterhelések mátrixa (ortogonális faktormegoldások esetén ismerjük $ \ bf A = P = S $). A regressziós módszer alapja a $ ^ 1 $ lábjegyzet.
Megjegyzés. Ez a $ \ bf B $ képlet PCA-val is használható: PCA-ban ugyanazt az eredményt adja, mint az előző szakaszban idézett képletek.
Az FA-ban (nem PCA-ban) a regressziós módon kiszámított faktorok pontszámai nem egészen "standardizáltak" lesznek - eltéréseik nem 1-esek lesznek, hanem megegyeznek a $ \ frac {SS_ {regr}} {(n-1)} $ értékkel ezeket a pontszámokat a változókkal regresszálva. Ez az érték úgy értelmezhető, mint egy tényező (valódi ismeretlen értékei) változók általi meghatározásának foka - az általuk reális tényező előrejelzésének R négyzete, és a regressziós módszer maximalizálja azt - a kiszámított "érvényessége". pontszámok. A $ ^ 2 $ kép a geometriát mutatja. (Felhívjuk figyelmét, hogy $ \ frac {SS_ {regr}} {(n-1)} $ megegyezik a pontszámok varianciájával bármely finomított módszer esetében, de csak a regressziós módszer esetében ez a mennyiség megegyezik a valódi f értékek meghatározásának arányával. f. pontszám alapján.)
A regressziós módszer változataként a $ \ bf R ^ * $ értéket használhatjuk a képletben $ \ bf R $ helyett. Indokolt, hogy egy jó faktoranalízisben a $ \ bf R $ és a $ \ bf R ^ * $ nagyon hasonlóak. Ha azonban nem, különösen akkor, ha a m tényezők száma kisebb, mint a tényleges populáció száma, a módszer erős torzítást eredményez a pontszámokban. És nem szabad ezt a "reprodukált R regressziós" módszert használni a PCA-val.
PCA-módszer , más néven Horst (Mulaik) vagy ideális (ized) változó megközelítés (Harman). Ez regressziós módszer, amelynek képletében $ \ bf \ hat R $ található a $ \ bf R $ helyett. Könnyen kimutatható, hogy a képlet ekkor $ \ bf B = (P ^ +) '$ -ra redukálódik (és így igen, valójában nem kell tudnunk vele $ \ bf C $ -ot). A tényező pontszámokat úgy számolják, mintha azok összetevő pontszámok lennének.
[Az "idealizált változó" címke abból adódik, hogy mivel a faktor vagy a modell komponens szerint a változók várható része $ \ bf \ hat X = FP '$, következik a $ \ bf F = (P ^ +)' \ hat X $, de a $ \ bf X $ -ot az ismeretlen (ideális) $ \ bf \ hat X $ -ra cseréljük, megbecsülni a $ \ bf F $ pontokat $ \ bf \ hat F $; ezért "idealizáljuk" $ \ bf X $.]
Felhívjuk figyelmét, hogy ez a módszer nem adja át a PCA komponensek pontszámát a tényező pontszámoknál, mert az alkalmazott terhelések nem a PCA terhelései, hanem faktoranalízisek '; csak a pontszámok számítási megközelítése tükrözi a PCA-ban ezt.
Bartlett-módszer . Itt $ \ bf B '= (P'U_2 ^ {- 1} P) ^ {- 1} P' U_2 ^ {- 1} $. Ez a módszer arra törekszik, hogy minden válaszadó esetében minimalizálja az p egyedi ("hiba") tényezők közötti különbségeket. Az így kapott közös tényező pontszámok eltérései nem lesznek egyenlőek, és meghaladhatják az 1.
Anderson-Rubin módszert az előző módosításaként fejlesztették ki. $ \ bf B '= (P'U_2 ^ {- 1} RU_2 ^ {- 1} P) ^ {- 1/2} P'U_2 ^ {- 1} $. A pontszámok varianciája pontosan 1. Ez a módszer azonban csak az ortogonális faktor megoldásokra vonatkozik (ferde megoldások esetén még mindig ortogonális pontszámokat eredményez).
McDonald-Anderson-Rubin módszer erős>. McDonald kiterjesztette Anderson-Rubint a ferde tényezők megoldására is. Tehát ez általánosabb. Ortogonális tényezőkkel valójában Anderson-Rubinra redukálódik. Egyes csomagok valószínűleg a McDonald's módszert használják, miközben "Anderson-Rubin" -nak hívják. A képlet: $ \ bf B = R ^ {- 1/2} GH 'C ^ {1/2} $, ahol $ \ bf G $ és $ \ bf H $ a $ \ text {svd} \ bf (R ^ {1/2} U_2 ^ {- 1} PC ^ {1/2}) = G \ Delta H '$. (Természetesen csak a $ \ bf G $ első m oszlopait használja.)
Green módszere . Ugyanazt a képletet használja, mint McDonald-Anderson-Rubin, de a $ \ bf G $ és $ \ bf H $ kiszámítása: $ \ text {svd} \ bf (R ^ {- 1/2} PC ^ {3/2 }) = G \ Delta H '$. (Természetesen csak az első m oszlopokat használja a $ \ bf G $ -ban.) Green módszere nem használ kommulalitási (vagy egyediségi) információkat. A McDonald-Anderson-Rubin módszerhez közelít és konvergál, mivel a változók tényleges közösségisége egyre egyenlőbbé válik. Ha pedig a PCA betöltésekor alkalmazzuk, akkor Green a komponens pontszámokat adja vissza, például a natív PCA módszerét.
Krijnen és mtsai módszer . Ez a módszer egy általánosítás, amely az előző kettőt egyetlen képlettel befogadja. Valószínűleg nem ad hozzá új vagy fontos új funkciókat, ezért nem fontolgatom.
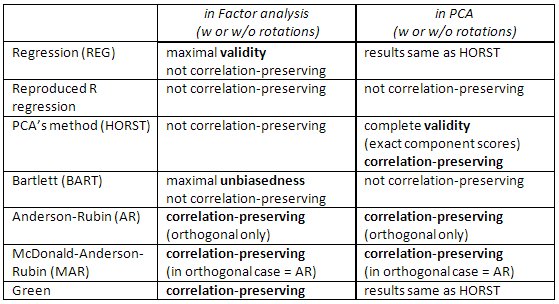
A finomított módszerek összehasonlítása .
-
Regresszió módszer maximalizálja a korrelációt a faktorok és a nem ismert valódi értékek között (vagyis maximalizálja a statisztikai érvényességet ), de a pontszámok kissé elfogultak és kissé helytelenül korrelálnak a tényezők között (pl. akkor is korrelálnak, ha a megoldás tényezői ortogonálisak) Ezek a legkisebb négyzetek becslései.
-
A PCA módszere szintén legkevesebb négyzet, de kisebb statisztikai érvényességgel. Gyorsabban kiszámíthatók; manapság a számítógépek miatt nem használják gyakran a faktorelemzésben. (A PCA ban ez a módszer natív és optimális.)
-
Bartlett pontszámai elfogulatlanok a valódi tényezőértékek becslései. A thescorusokat úgy számolják, hogy pontosan korreláljanak más tényezők valódi, ismeretlen értékeivel (pl. Hogy ne korreláljanak velük például ortogonális oldatban). Mindazonáltal pontatlanul korrelálhatnak a más tényezőkre kiszámított faktor pontszámokkal . Ezek maximális valószínűségű (a $ \ bf X $ feltételezés többváltozós normalitása mellett) becslések.
-
Anderson-Rubin / McDonald-Anderson -Rubin és Green pontszámokat korrelációmegőrzés nek nevezzük, mivel úgy vannak kiszámolva, hogy pontosan korreláljanak más tényezők faktorértékeivel. A faktor-pontszámok közötti korrelációk megegyeznek az oldatban szereplő tényezők közötti korrelációval (így például ortogonális megoldásnál a pontszámok tökéletesen korrelálatlanok lesznek). De a pontszámok kissé elfogultak, és érvényességük szerény lehet.
Ellenőrizze ezt a táblázatot is:
[Megjegyzés az SPSS-felhasználók számára: Ha PCA t („fő összetevők” kivonási módszert) végez, de a „Regresszió” metódustól eltérő kérési tényező pontszámok vannak érvényben, a program figyelmen kívül hagyja a kérést és kiszámítja te inkább "regressziós" pontszámokat kapsz (amelyek pontos összetevői pontszámok).]
Referenciák
-
Grice, James W. A faktorszámok kiszámítása és értékelése // Pszichológiai módszerek 2001, Vol. 6, 4. szám, 430-450.
-
DiStefano, Christine és mtsai. Faktor-pontszámok megértése és felhasználása // Gyakorlati értékelés, Research & Evaluation, Vol 14, No 20
-
ten Berge, Jos M.F.et al. Néhány új eredmény a korreláció-megőrző faktor pontszámok előrejelzési módszerein // Linear Algebra and its Applications 289 (1999) 311-318.
-
Mulaik, Stanley A. A faktoranalízis alapjai, 2. kiadás, 2009
-
Harman, Harry H. Modern tényezők elemzése, 3. kiadás, 1976
-
Neudecker, Heinz. A faktor-pontszámok legjobb affin elfogulatlan kovariancia-megőrző előrejelzéséről // SORT 28 (1) 2004. január-június, 27-36
$ ^ 1 $ több lineáris regresszióban, központosított adatokkal figyelhető meg, hogy ha $ F = b_1X_1 + b_2X_2 $, akkor $ s_1 $ és $ s_2 $ kovariancia $ F $ és a prediktorok között:
$ s_1 = b_1r_ {11 } + b_2r_ {12} $,
$ s_2 = b_1r_ {12} + b_2r_ {22} $,
ahol $ r $ s a kovariancia a $ X $ s között . Vektoros jelölésben: $ \ bf s = Rb $. A tényező $ F $ kiszámításának regressziós módszerében a $ b $ s értéket az ismert ismert $ r $ s és $ s $ s értékekből becsüljük.
$ ^ 2 $ A következő kép mind a itt képek egyben vannak kombinálva. Megmutatja a különbséget a közös tényező és a fő komponens között. A komponens (vékony piros vektor) a változók (két kék vektor) által átfogott térben található, fehér "X sík". A faktor (zsírvörös vektor) felülírja ezt a teret. A faktor síkra eső ortogonális vetülete (vékony szürke vektor) a regresszíven becsült faktor-pontszám. A lineáris regresszió definíciója szerint a faktor pontszámok a legjobbak, a legkisebb négyzetek szempontjából a változók által elérhető tényező közelítése.